• 试题分析
• 复习路线
  • 级数
    • 1.数项级数敛散性判别：
    • 2.幂级数的收敛半径和收敛域：
    • 3.幂级数的和函数：
    • 4.幂级数展开：
    • ⭐5.表格积分法秒杀傅里叶级数：
    • 6.级数证明题（积累）：
  • 多元函数微分学
  • 重积分和曲线曲面积分
    • 1.灵活利用对称性：
    • ⭐2.合一投影法替换高斯定理：
    • 记住一些常用的结论：

b站大学系列之20分钟速通微积分

试题分析

级数：40%

重积分和曲线曲面积分：40%

多元函数微分学：20%

从知识点所占的分值来看，级数占据主导地位，所以应该优先复习，多元函数微分学较易可以少花时间，重积分和曲线曲面积分计算量较大。建议往年题只做最近3年的，做多了绝对是浪费时间，还不如看看我总结的一些做题技巧，考前可以多做几道级数的证明题和复杂的积分题。

复习路线

级数 - 多元函数微分学 - 重积分 和曲线曲面积分

级数

1.数项级数敛散性判别：

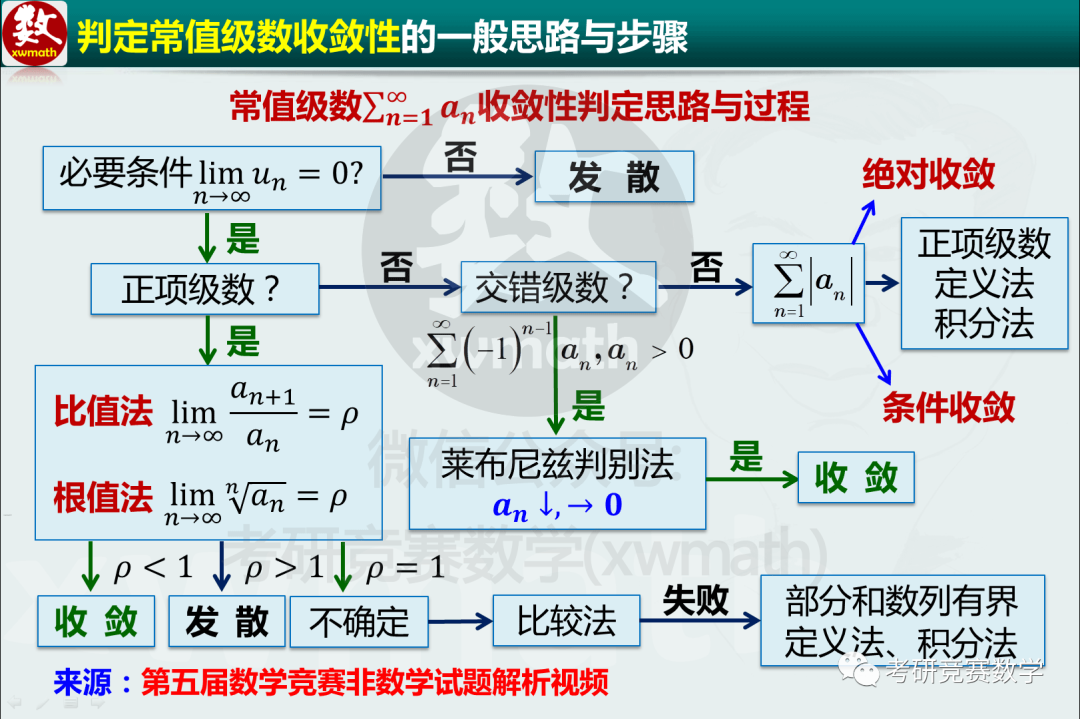
选择题记住级数$q^{n},\frac{1}{n^{p}},\frac{1}{n(lnn)^{p}}$什么时候收敛直接用等价无穷小替换估计一下就行，如果出现$n!$，也可以考虑使用斯特林公式，。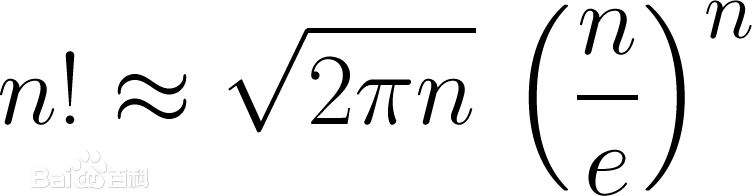

2.幂级数的收敛半径和收敛域：

1.收敛区间为开区间，求收敛域时要考虑端点的敛散性。

2.对于缺项的幂级数，如只有奇次幂或只有偶次幂的幂级数，可以用一般的函数项级数收敛域的计算方法或者换元。

3.幂级数的和函数：

先求出幂级数的收敛半径和收敛域，然后利用已知幂级数的和函数，通过逐项求导或逐项积分来求。

注：如果比较熟练，可以不设和函数表达式，最终的和函数记得带上收敛域。

4.幂级数展开：

一般采用间接法，利用$e^{x},sinx,\frac{1}{1+x},ln(1+x)$来求其它函数的幂级数展开。

⭐5.表格积分法秒杀傅里叶级数：

在求傅里叶系数的时候，肯定会用到分部积分法，但是这个过程非常复杂，可以用表格积分法来提高计算速度。

表格积分法步骤：别再用分部积分法了，表格法秒杀

6.级数证明题（积累）：

证明题都非常灵活，需要多加练习，拓展思维。

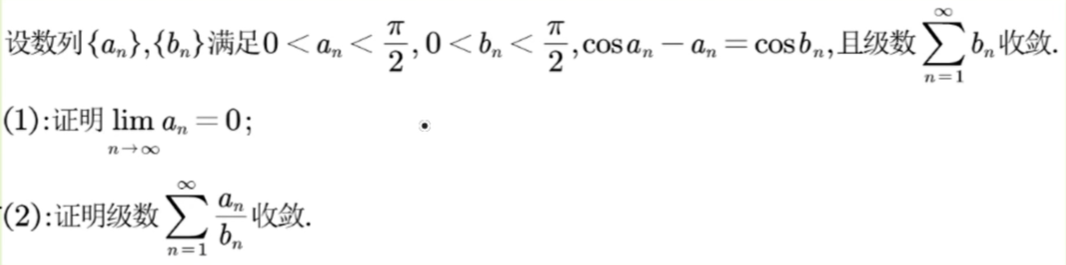
多元函数微分学

这一部分非常简单，主要会考察基本的概念，求偏导，切线，法平面，梯度，极值问题。

重积分和曲线曲面积分

1.灵活利用对称性：

• 二重积分的轮换对称性

  

  第一个结论会经常用到，比如下面这道例题用第一个结论就会非常简单：

  

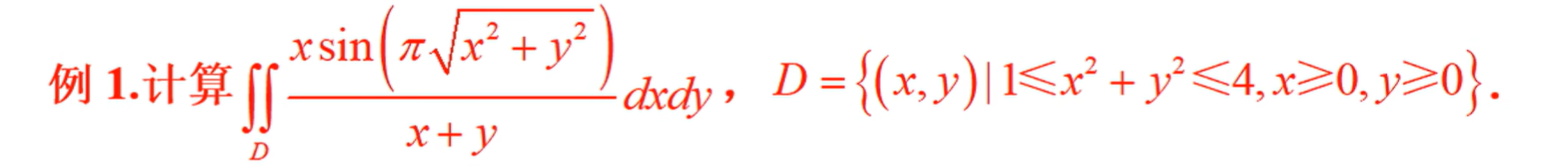
• 下面两道题也是轮换对称性，第一题把$3z^{2}$拆成$z^{2}+2z^{2}$,算一下的话是16$\pi$,第二题选D。

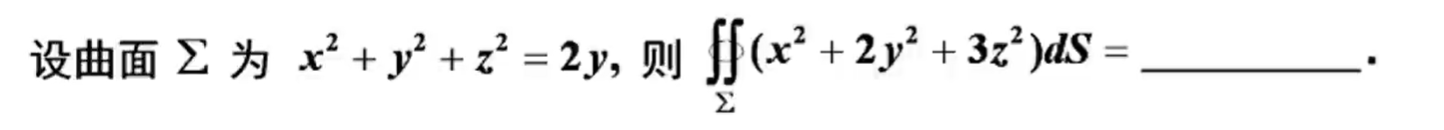
⭐2.合一投影法替换高斯定理：

上面是我期中复习时写的，直接搬过来，也可以参考b站上的讲解视频链接

记住一些常用的结论：

1.第一类曲面积分投影面积元的关系

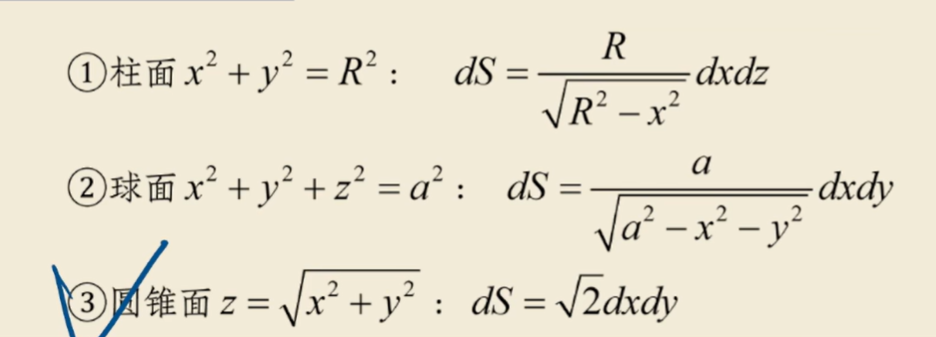
2.有的话再补充